9.1. Concatenative speech synthesis#
Concantenative speech synthesis (CSS), also known as unit selection speech synthesis, is one of the two primary modern speech synthesis techniques together with statistical parametric speech synthesis. As the name suggests, CSS is based on concatenation of pre-recorded speech segments in order to create intelligible high-quality speech. The advantage of this approach is extremely high naturalness of the produced speech, as long as the system is well-designed and suitable speech data are available for its development. The drawback is limited flexibility as all the used speech segments have to be pre-recorded, limiting the choice of speaker voices or other modifications to the verbal expression.
The most simple CSS system imaginable could be developed using concatenation of pre-recorded word waveforms. However, as [Rabiner and Schafer, 2007] note, such an approach would suffer from two primary problems. First, concatenation of word-level waveforms would sound unnatural, as coarticulatory effects between words would be absent from the data. In addition, the system would be limited to very restrictive scenarios only, as there can be tens or hundreds of thousands of lexical items and millions of proper names in any language—way more than what can be reasonably pre-recorded by any individual speaker. The problem is even worse for agglutinative languages such as Finnish, where word meanings are constructed and adjusted by extending word root forms with various suffixes. Since words can also participate to utterances in various positions and roles, prosodic characteristics (e.g., F0) of the same word can differ from context to another. This means that pre-recording all possible words is not a practical option.
To solve the issues of scalability and coarticulation, practical modern CSS systems are based on sub-word units. In principle, there are only few phones per language (e.g., around 40–50 for English), but their acoustic characteristics are also highly dependent on the surrounding context due to coarticulation. Context-dependent phones such as diphones (pairs of phones) or triphones (phone triplets) are therefore utilized. In order to build a CSS system, speech dataset has to be first carefully annotated and segmented for the units of interest. These segments can then be stored as acoustic parameters (e.g., speech codec parameters) to save space and to allow easy characterization and manipulation.
9.1.1. Steps of concatenative synthesis#
Once a database of units exists, synthesis with CSS consists of the following basic steps: 1) conversion of input text to a target specification, which includes the string of phones to be synthesized together with additional prosodic specifications such as pitch, duration, and power, 2) unit selection for each phone segment according to the specification, and 3) post-processing to reduce the impact of potential concatenation artefacts.
While the text processing stage is largely similar to pre-processing in statistical parametric speech synthesis systems, the main part of CSS is to perform unit selection in such a manner that the output speech matches the specification with high naturalness of the sound. As described by [Hunt and Black, 1996], unit selection is achieved by cost minimization using two cost functions (Fig. 1): target cost \(C^{t}(u_{i},t_{i})\) and concatenation cost \(C^{c}(u_{i-1},u_{i})\). Target cost describes the mismatch between the target speech unit specification \(t_{i}\) and a candidate unit \(u_{i}\) from the database. Concatenation cost describes the mismatch (e.g., acoustic or perceptual) of the join between the candidate unit \(u_{i}\) and the preceding unit \(u_{i-1}\). In other words, an ideal solution would find all the target units according to the specification without introducing acoustic mismatches at the edges of concatenated units.
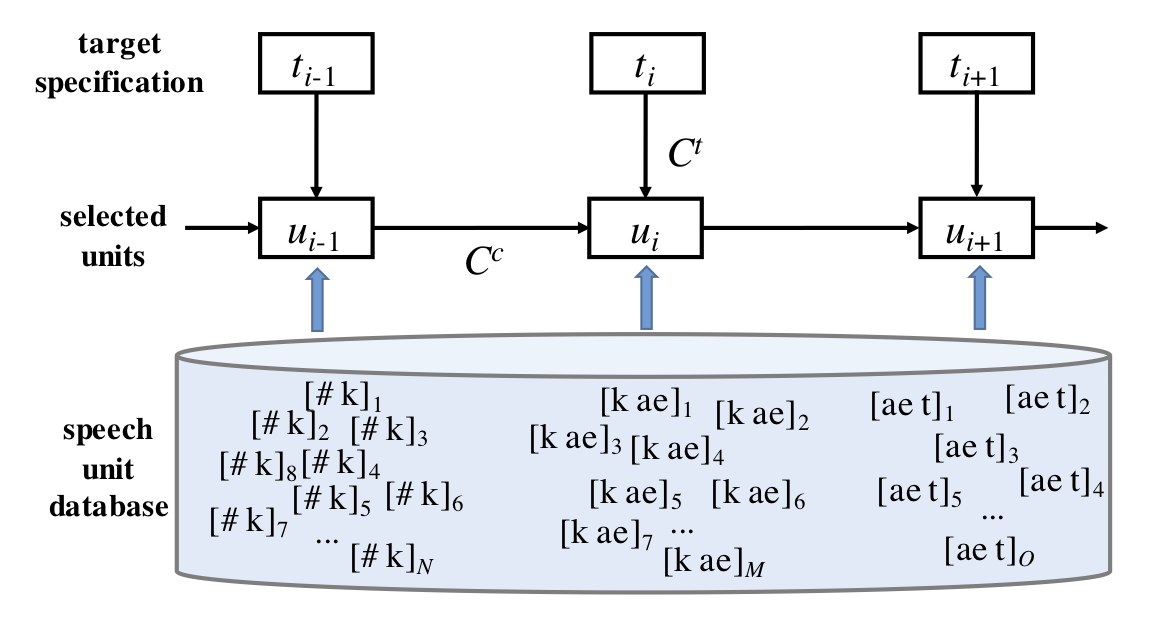Figure 1: An illustration of the selection cost Ct and concenation cost Cc in diphone-based unit selection for synthesis of word “cat” [k ae t]. In practice, diphones with different initial phones but similar coarticulatory effects on the target phone can be considered in the selection process to overcome the issue of data sparsity. Adapted from [Hunt and Black, 1996].
Since the target specification consists of many characteristics such as target and context phone(s) identity, pitch, duration, and power, the target cost can be divided into multiple subcosts \(j\) as \( C_{j}^{t}(t_{i},u_{i}) \) . For instance, the contextual phone(s) (e.g., [ae] in the last unit [ae t] of “cat” in Fig. 1) can be represented by a number of features describing the manner and place of articulation, so that the specification can be compared to different candidate units in the database [Hunt and Black, 1996]. This enables the use of different context phones with similar coarticulatory effects on the target phone. Similarly, costs for segment power and pitch can be measured, e.g., in terms of the differences in mean log-power and mean F0. Cost for the target phone ([t] in [ae t] of Fig. 1) is usually a binary indicator that forces the phonemic identity of the chosen unit to match with that of the target specification. The total cost can then be written as
(1)
where \(w^{t} = [w^{t}_{1}, w^{t}_{2}, ..., w^{t}_{P}]\) are the relative weights of each subcost.
Concatenation cost \(C^{c}(u_{i-1},u_{i})\) can be derived in a similar manner to Eq. (1) by decomposing the the total cost to \(Q\) subcosts, and then calculating a weighted sum of the subcosts:
(2)
Note that the subcosts and their weights \(w^{c}\) for \(C^{c}\) do not need match those of \(C^{t}\), as the concatenation cost specifically focuses on the acoustic compatibility of the subsequent units. Therefore subcosts \(C^{c}_{j}(u_{i-1},u_{i})\) associated with continuity of the spectrum (or cepstrum), segment power, and pitch in the segment and/or at the concenation point should be considered.
The total cost of the selection process is the sum of the target and concenation costs across all \(n\) units:
(3)
where \( t_{1}^{n} \) are the targets, \( u_{1}^{n} \) are the selected units, and # denotes silence [Hunt and Black, 1996]. The two extra terms stand for transition from preceding silence to the utterance and from utterance to the trailing silence. The aim of the selection process is then to find units \( \bar{u}_{1}^{n} \) that minimize the total cost in Eq. (3). The selection process can be represented as a fully connected trellis, as shown in Fig. 3, where each edge to a node has a basic cost of the given node to be chosen (the target cost) and an additional cost depending on the previous unit (the concatenation cost). Given the trellis, the optimal selection can be carried out with Viterbi search—a dynamic programming algorithm that calculates the least cost path through the trellis. To make the search computationally feasible for large databases, less likely candidates for each target can be pruned from the trellis. In addition, beam search with only a fixed number of most likely nodes for each step can be applied for further speedup.
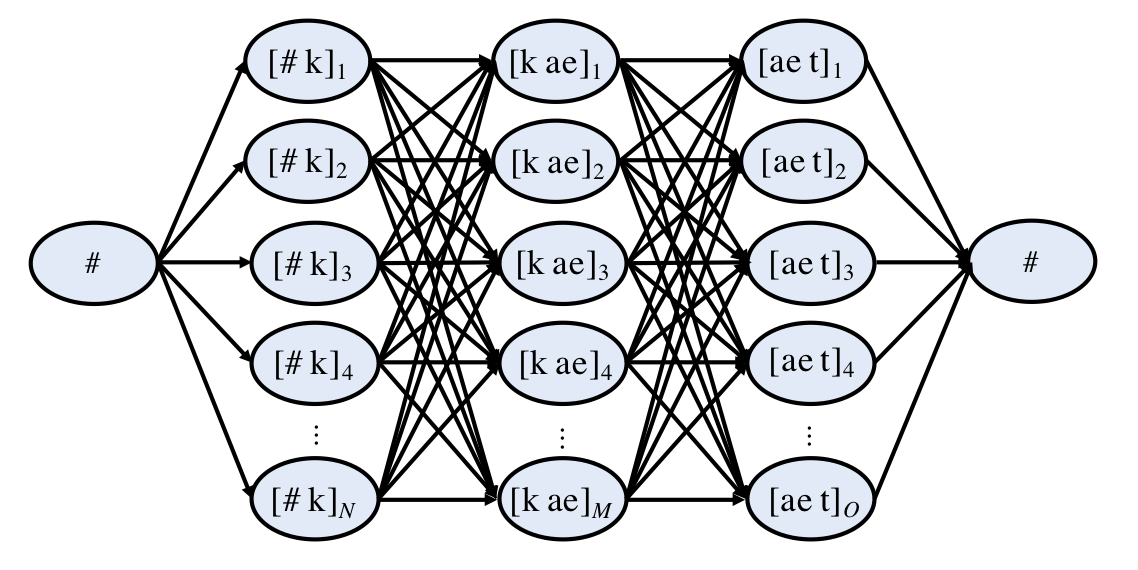
Figure 3: An example of unit selection search trellis for word “cat” [k ae t]. Each edge is associated with basic target cost of the selected unit and concatenation cost dependent on the previous unit. Adapted from [Rabiner and Schafer, 2007]
After the speech units have been concatenated to form the intended utterance, postprocessing techniques can be used to smooth the potential discontinuities in F0, energy and spectrum at the unit boundaries. Note that aggressive signal processing based modification of the segments also often tends to decrease the naturalness of the sound. Straightforward modification of the segments’ acoustic parameters (e.g. with vocoding) is not therefore a recommended strategy to overcome the issues of poor unit selection or low quality source data.
9.1.2. CSS training#
The above formulation enables mathematically principled and optimal unit selection process from a given speech database. However, the synthesis output is highly dependent on the choice of features and functions used for the subcosts, and also on the weights chosen for each feature. While the cost functions and their underlying features can be largely designed based on knowledge in signal processing and speech processing, the weights need to be either adjusted through trial and error, or they can be automatically optimized using some kind of quality criterion.
As examples of automatic weight estimation, [Hunt and Black, 1996] propose two alternative ways to automatically acquire cost function weights:
1) Using a grid search across different weight values by synthesizing utterances using the target specifications of held-out utterances from the training database, and then comparing the synthesized waveform to the real waveform of the held-out utterance using an objective metric. The weights that lead to the best overall performance are then chosen.
2) Using regression models to predict best values for the weight. [Hunt and Black, 1996] report that cepstral distance and power difference across the concanation point can be used as predictors for reported perceptual quality of the concatenation in a linear regression model, and therefore the linear regression weights can be directly used as perceptually motivated the cost weights. For the target weights, they propose and approach where each unit in the database is considered as the target specification at a time, and \(K\) best matching other units are then searched for the target using an objective distance measure. Then the sub-costs between the target and the \(K\) matches are calculated and recorded. This process is repeated for all exemplars of the same phonetic unit in the database, recording the \(K\times Q\) subcosts and the related \(K\) distances for each exemplar. Linear regression is then applied to predict the recorded objective perceptual distances using the associated sub-costs, linear regression coefficients again revealing the optimal weights for each of the subcosts. A specific advantage of the regression approach for subcost weight estimation is that it allows estimation of phoneme-specific weights for each subcost, as the perceptually critical cues may differ from a phonetic context to another.
9.1.3. Further reading#
- HB96(1,2,3,4,5,6)
Andrew J Hunt and Alan W Black. Unit selection in a concatenative speech synthesis system using a large speech database. In 1996 IEEE International Conference on Acoustics, Speech, and Signal Processing Conference Proceedings, volume 1, 373 – 376. IEEE, 1996. URL: https://doi.org/10.1109/ICASSP.1996.541110.
- RS07(1,2)
Lawrence R Rabiner and Ronald W Schafer. Introduction to digital speech processing. Foundations and Trends in Signal Processing, 1(1):1 – 194, 2007. URL: https://doi.org/10.1561/2000000001.