3.13. Pitch-Synchoronous Overlap-Add (PSOLA)#
Many speech applications require the ability to modify the fundamental frequency. For a classic but marginal application, think of the auto-tune function often used in post-processing of singing voices. With such tools it is possible to change the fundamental frequency of a speaker’s or singer’s voice without changing the phoneme or timbre of the sound. One of the more popular tools developed for this purpose is pitch-synchronous overlap-add (PSOLA). Like the name suggests, it is closely related to the overlap-add method used in the short-time Fourier transform algorithm. It allows changing the pitch of a speech sound without modifying or with only minor influence on other characteristics of the signal, such as vowel-identity. In addition to auto-tune, an important application of PSOLA is speech synthesis, where we want to be able generate speech with any reasonable pitch contour. Voice conversion is another application, where the objective is to convert the speech of one person, such that it sounds like speech of another person.
Illustration of the PSOLA process; find period length and maximum peak in each period.
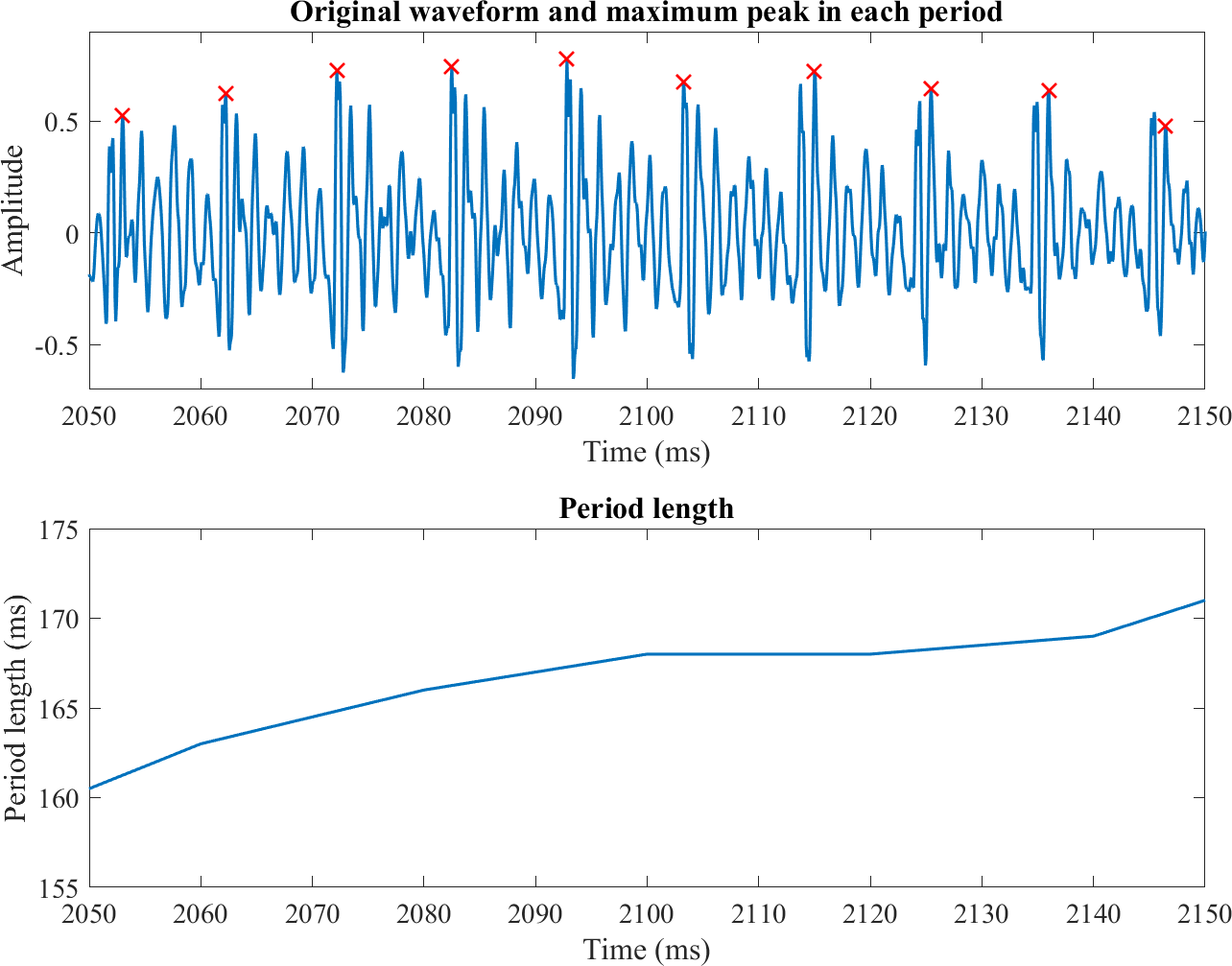
The basic idea of PSOLA is to decompose the signal into individual pitch-periods, such that we can move the pitch-periods to change the effective length of those periods. That is, the fundamental frequency of a signal is expressed as a periodic structure of the time-signal. If we cut the signal into segment corresponding to the length of such periodic structures, then we can shift their positions as desired and then add them back together, like in the overlap-add process (see STFT). Since short-term correlations in the signal are not changed, that is, signal inside the windows/segments is not changed, then the spectral envelope of the signal is not changed.
PSOLA analysis windowing, time-shift and synthesis windowing
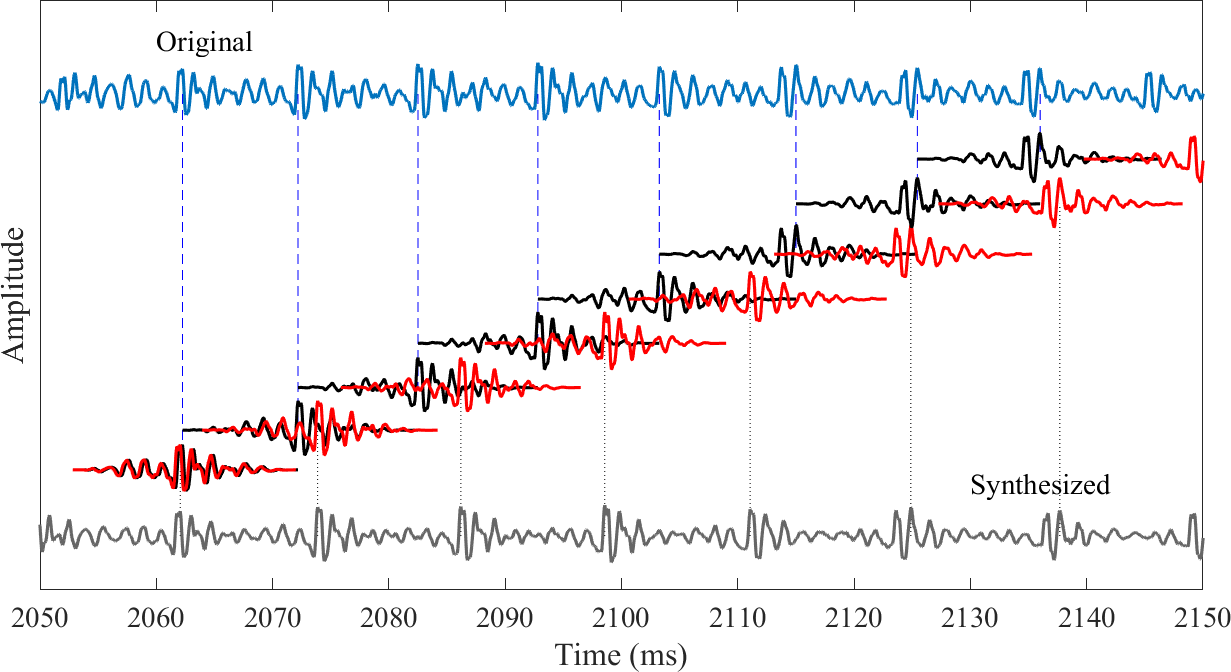
To illustrate the principle, consider the following basic algorithm:
Estimate the fundamental frequency contour of a speech sample.
Find pitch periods of the speech sample, for example by identifying the largest peak in each period.
Extract windows of the speech signal covering two pitch periods. Apply a windowing function with perfect reconstruction. (Observe: Perfect reconstruction should apply for each period, so we construct half-length windows for each period. Conversely, the left and right parts of windows can be of different length.)
Shift windows to match the desired pitch-period length.
In the sound examples on the right, the pitch period lengths are adjusted by a fixed multiplier to increase or decrease the fundamental frequency. Observe that the implementation is not perfectly tuned such that the output sound has some audible distortions.
Sound examples with varying multiplier on distance between pitch periods
Show code cell source
import IPython.display as ipd
print('Multiplier 0.6')
ipd.display(ipd.Audio('attachments/175514533.wav'))
print('Multiplier 0.8')
ipd.display(ipd.Audio('attachments/175514532.wav'))
print('Multiplier 0.9')
ipd.display(ipd.Audio('attachments/175514531.wav'))
print('Multiplier 1.0 (original)')
ipd.display(ipd.Audio('attachments/175514530.wav'))
print('Multiplier 1.1')
ipd.display(ipd.Audio('attachments/175514529.wav'))
print('Multiplier 1.2')
ipd.display(ipd.Audio('attachments/175514528.wav'))
print('Multiplier 1.4')
ipd.display(ipd.Audio('attachments/175514527.wav'))
Multiplier 0.6
Multiplier 0.8
Multiplier 0.9
Multiplier 1.0 (original)
Multiplier 1.1
Multiplier 1.2
Multiplier 1.4


