4.1. Pre-emphasis#
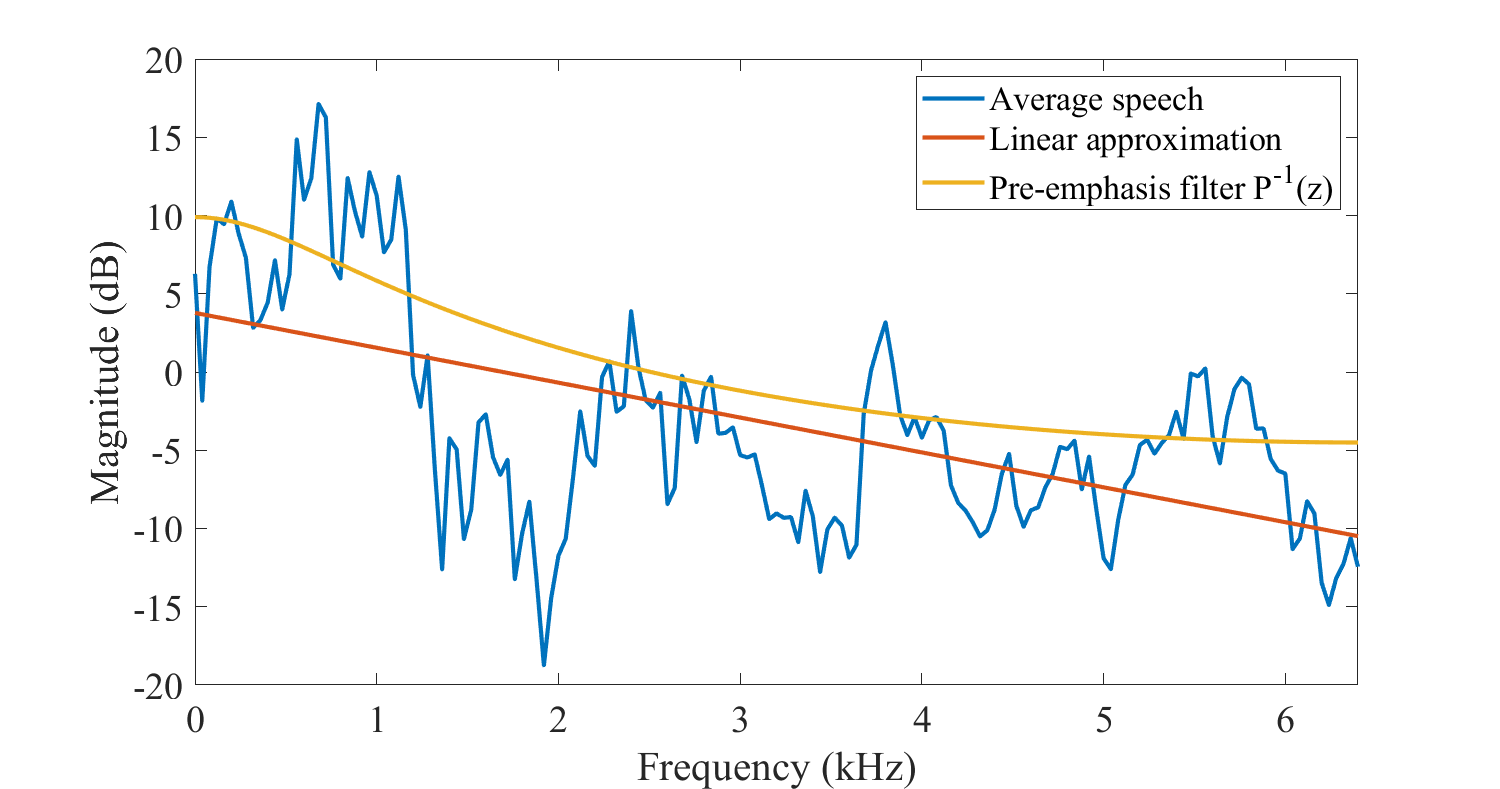
The figure above illustrates the average magnitude spectrum of a speech signal. We observe that a majority of the energy is concentrated in the lower end of the spectrum. In fact, as a linear approximation, we see that in this particular example, the energy drops at a rate of 2.2 dB/kHz. The exact rate of decrease varies for each speaker and depending on several factors. A safe and often used assumption is that energy drops at roughly 2 dB/kHz.
This rapid reduction in energy leads to practical problems in implementations. For example, if we would implement a discrete Fourier transform with fixed-point arithmetic, then the accuracy would be very different in different parts of the spectrum. Typically the spectrum at 6kHz is 15dB lower than at 0Hz. On a linear scale 15dB corresponds to a factor of 6. In other words, on a 16-bit CPU, if we use the full range of a signed 15-bit representation for the lowest frequencies, than we use effectively only 12-bit range for frequency components at 6kHz.
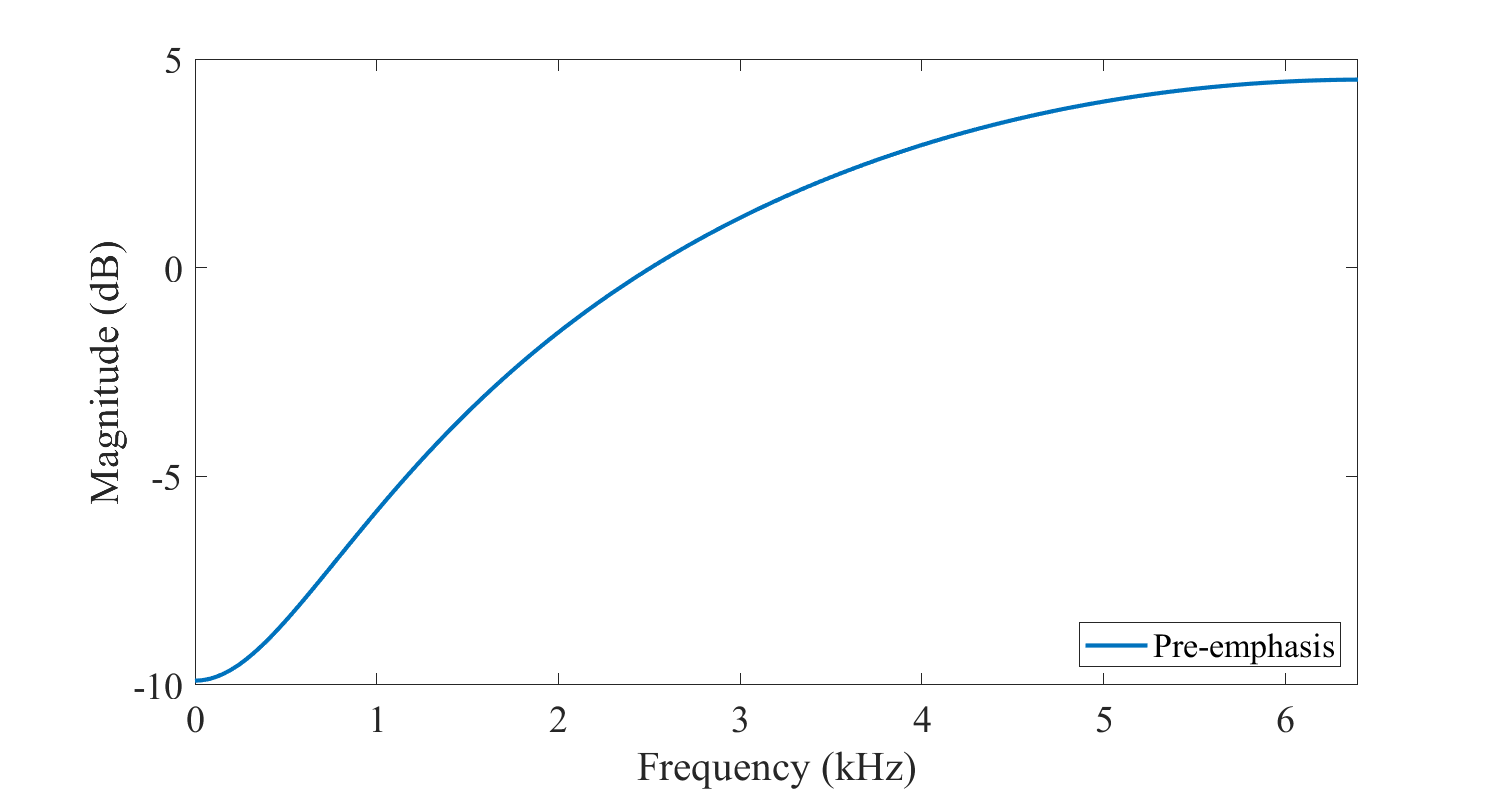
A common pre-processing tool used to compensate for the average spectral shape is pre-emphasis, which emphasises higher frequencies. Typically, pre-emphasis is applied as a time-domain FIR filter with one free parameter, for example, in speech coding at a sampling rate of 8kHz or 12.8kHz, we use the pre-emphasis filter \( P(z)=1-0.68 z^{-1} \) [Bäckström et al., 2017]. The spectrum of this filter is illustrated below. After applying the filter, the spectrum is more flat and we can apply fixed-point arithmetic with a lower accuracy and thus better optimize CPU consumption.
There are numerous different ways of tuning pre-emphasis. Firstly, though the average spectrum is decaying, unvoiced fricatives have typically more energy at the high frequencies. Excessive pre-emphasis would therefore cause problems for fricatives. Pre-emphasis also has an effect on both perceptual and statistical modelling as well as estimation of linear predictive models. The best amount of pre-emphasis is therefore very much dependent on the application and implementation details.
4.2. References#
Tom Bäckström, Jérémie Lecomte, Guillaume Fuchs, Sascha Disch, and Christian Uhle. Speech coding: with code-excited linear prediction. Springer, 2017. URL: https://doi.org/10.1007/978-3-319-50204-5.
