11.8.3. Time-Delay of Arrival (TDoA) and Direction of Arrival (DoA) Estimation

In multi-channel speech enhancement, a regularly appearing task is to estimate the time-delay between channels or equivalently, the angle at which a wavefront arrives to an array of microphones. By knowing the time-delay or angle of arrival, we can use beamforming to isolate sounds from that particular direction. A frequently used method for time-delay estimation is the generalized cross-correlation (GCC) method and especially its PHAT-weighted variant known as GCC-PHAT [Azaria and Hertz, 1984, Knapp and Carter, 1976, Kwon et al., 2010].

11.8.3.1. Generalized cross-correlation

The cross-spectrum of two spectra \(X_{1,k,t}\) and \(X_{2,k,t}\) is

\[ C_{k,t} = X_{1,k,t}^* X_{2,k,t}, \]

where \(k\) and \(t\) are the frequency and time indices. The spectra are of form \(X_{h,k}=a_{h,k} e^{i\frac{2\pi kn_h}N}\), where \(n_h\) is the time-offset and \(N\) is the length of the analysis window. We thus have

\[ C_k = a_{1,k} e^{-i\frac{2\pi kn_1}N} a_{2,k} e^{i\frac{2\pi kn_2}N} . \]

If the time-difference between channels is \(\tau=n_2-n_1\), then

\[ C_k = a_{1,k}a_{2,k} e^{-i\frac{2\pi kn_1}N+i\frac{2\pi k(\tau+n_1)}N} = a_{1,k}a_{2,k} e^{i\frac{2\pi k\tau}N} . \]

It can be weighted with a variety of approaches such as

\[ C_k' = \frac{X_{1,k}^* X_{2,k}}{|X_{1,k}^* X_{2,k}|} = e^{i\frac{2\pi k\tau}N} \]

to obtain the generalized cross-spectrum. The generalized cross-correlation is the inverse Fourier transform of the generalized cross-spectrum

\[ r_k' = {\mathcal F}^{-1}\{C_k'\} = \delta_\tau, \]

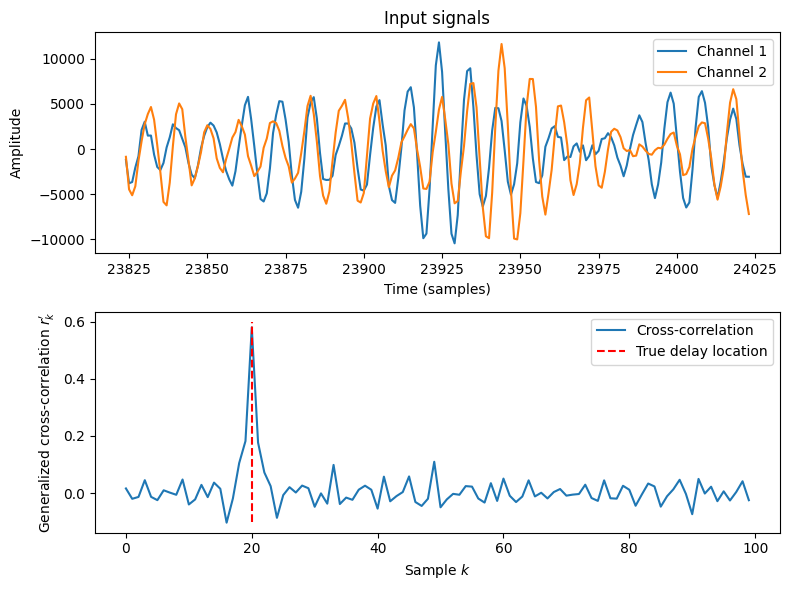
where \(\delta_k\) is the Dirac-delta function. In other words, the generalized cross-covariance has a single peak whose position indicates the time-delay \(\tau\) between the two channels.

Show code cell source Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
from scipy.io import wavfile
import scipy
import IPython.display as ipd
from helper_functions import stft

# read from storage
filename = 'sounds/temp.wav'
fs, data = wavfile.read(filename)

delay_samples = 20
delay_zeros = np.zeros(delay_samples)

data1 = np.concatenate((data,delay_zeros))
data2 = np.concatenate((delay_zeros,data))

noise_gain_dB = -10
noise_gain = np.std(data)*10**(noise_gain_dB/20)

observation1 = data1 + noise_gain*np.random.randn(len(data1))
observation2 = data2 + noise_gain*np.random.randn(len(data1))

X1 = stft(observation1,fs)
X2 = stft(observation2,fs)

crossspectrum = np.mean(np.conj(X1)*X2,axis=0)
crosscorrelation = scipy.fft.irfft(crossspectrum/np.abs(crossspectrum))

Show code cell source Hide code cell source

plt.figure(figsize=[8,6])
plt.subplot(211)
ix = np.argmax(observation1)
plt.plot(range(ix-100,ix+100),observation1[(ix-100):(ix+100)],label='Channel 1')
plt.plot(range(ix-100,ix+100),observation2[(ix-100):(ix+100)],label='Channel 2')
plt.xlabel('Time (samples)')
plt.ylabel('Amplitude')
plt.legend()
plt.title('Input signals')

plt.subplot(212)
plt.plot(crosscorrelation[0:100],label='Cross-correlation')
plt.plot([delay_samples,delay_samples],[-.1,.6],'r--',label='True delay location')
plt.legend()
plt.xlabel('Sample $k$')
plt.ylabel("Generalized cross-correlation $r_k'$")

plt.tight_layout()
plt.show()

11.8.3.2. References

AH84

Mordechai Azaria and David Hertz. Time delay estimation by generalized cross correlation methods. IEEE Transactions on Acoustics, Speech, and Signal Processing, 32(2):280 – 285, 1984. URL: https://doi.org/10.1109/TASSP.1984.1164314.

KC76

C. Knapp and G. Carter. The generalized correlation method for estimation of time delay. IEEE Transactions on Acoustics, Speech, and Signal Processing, 24(4):320–327, 1976. doi:10.1109/TASSP.1976.1162830.

KPP10

Byoungho Kwon, Youngjin Park, and Youn-sik Park. Analysis of the GCC-PHAT technique for multiple sources. In ICCAS 2010, volume, 2070–2073. 2010. doi:10.1109/ICCAS.2010.5670137.